Synchronizacja zegarów stanowi fundamentalny punkt szczególnej teorii względności. Każdy punkt w czasoprzestrzeni jest teoretycznie wyposażony w wirtualny zegar i pozostaje tylko zsynchronizować je, aby otrzymać informację o kolejności zdarzeń. W tym celu wysyłamy sygnał świetlny do punktu zaopatrzonego w zegar i czekamy na jego natychmiastową odpowiedź również w postaci impulsu świetlnego.
W momencie jego powrotu znamy opóźnienie zegara, który synchronizowaliśmy co wystarcza nam do określenia pojęcia następstwa i jednoczesności zdarzeń. Należy podkreślić, że synchronizujemy zegary tylko w obrębie tego samego układu inercjalnego.
Już Einstein w swojej pracy „On the Electrodynamics of Moving Bodies” zauważył, że warunek aby sygnał świetlny biegł w obie strony z tą samą prędkością nie jest konieczny. W rzeczywistości możemy jedynie obserwować prędkość światła na drodze zamkniętej, gdzie oczywiście v = 2AB / t.
Możemy uporządkować opis tych synchronizacji wprowadzając współczynnik Reichenbacha

Wtedy prędkość światła wyrazi się wzorem
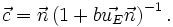
W powyższych wzorach wprowadziliśmy czteroprędkość uE. Jest to czteroprędkość pewnego wyróżnionego względem nas układu odniesienia tak zwanego układu preferowanego. Wektor 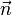 jest jednostkowym wektorem kierunkowym wskazującym na synchronizowany zegar.
jest jednostkowym wektorem kierunkowym wskazującym na synchronizowany zegar.
Twierdzenie o konwencji synchronizacji mówi, że wybór współczynnika Reichenbacha jest arbitralny, oczywiście w połączeniu z warunkiem na stałość prędkości światła na drodze zamkniętej.
Z tego względu możemy mówić przynajmniej o dwóch rodzajach synchronizacji. Funkcja  pozwala w STW na wybór właściwej synchronizacji.
pozwala w STW na wybór właściwej synchronizacji.
- Synchronizacja standardowa nazywana także synchronizacją Einsteina-Poincaré, gdzie prędkość światła w obu kierunkach jest taka sama. W tym przypadku b = 0, więc

i otrzymujemy standardową postac transformacji Lorentza.
- Synchronizacja absolutna nazywana także synchronizacją Changa-Tangherliniego, gdzie prędkość światła zależy od kierunku.
Żądamy w tym przypadku, aby składowe czasowo-przestrzenne macierzy transformacji Lorentza spełniały warunek

wtedy otrzymujemy
 .
.
Współczynnik Reichenbacha wynosi wtedy

Natomiast prędkość światła
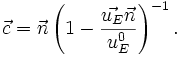
Źródło: Wikipedia (autorzy, na licencji CC-BY-SA 3.0)
